Here is to another curious and funny identity that has popped up many times and I’ve never quite gotten to find a proof for it:

$$ \sum_{n=0}^{N-1} \sin^2\left( x+ \frac{\pi}{N} n \right) = \frac{N}{2}, \; \forall N \in \mathbb{N} \geq 2$$

The Trigonometric Pythagorean Identity

What’s the connection to good old Pythagoras you ask? Well, let us look at it for $N=2$:

$$\sin^2 \left( x\right) + \sin^2\left( x + \frac{\pi}{2}\right) = 1$$

Since we can think of the cosine as a shifted version of the sine, where the shift is $\pi/2$, i.e., $\cos(x) = \sin(x+\pi/2)$, the last identity reads in fact as:

$$\sin^2 \left( x\right) + \cos^2\left( x \right) = 1$$

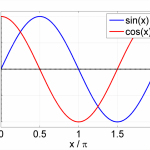
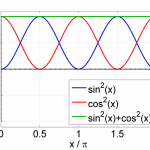
This may look familiar, in fact it is often referred to as the Trigonometric Pythagorean Identity (I’ll call it TPI for short). Here is a graphical illustration: On the left-hand side you see the sine and the cosine function, on the right-hand side their squares and the sum of the squares. They add up to a constant.

Analytical arguments aside what is the link to Pythagoras’ Theorem? Well, there is a nice geometric illustrations of this. Consider a right triangle with one of its angles $\theta$, the sides being $a$ (the adjacent), $b$ (the opposite) and $c$ (the hypotenuse). From Pythagoras Theorem we know that $a^2 + b^2 = c^2$. At the same time we know from the definition of the trigonometric functions that sine and the cosine are related to the ratio between adjacent (opposite) and hypotenuse. In equations:

$$ \sin(\theta) = \frac{b}{c} \\ \cos(\theta) = \frac{a}{c}$$

Squaring and summing gives:

$$ \sin(\theta)^2 + \cos(\theta)^2 = \frac{a^2}{c^2} + \frac{b^2}{c^2} = \frac{a^2+b^2}{c^2} = 1$$

which explains the link to Pythagoras (a more complete version of the argument that also works for obtuse angles can be found on wikipedia).

Extended TPI for N>2

Okay, that was very elementary and maybe even boring stuff. The cool thing is that this works under much more general settings. I have not found a real name of the identity above but you could see it as a straightforward generalization of the TPI. Instead of considering a squared sine and one shifted copy (i.e., summing the shifts 0 and $\pi/2$) you can consider a sum of $N$ shifted copies that still add up to a constant provided that the shifts are chosen uniformly (i.e., all integer multiples of $\pi/N$).

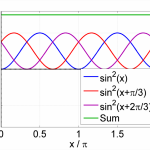
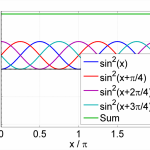
Here is a graphical illustration for $N=3$ and $N=4$:

Cool stuff, right? Well I think so. However, the actual question of this blog post is, how do we prove this?

Proof idea 1: Decomposing into interleaved sums

This is the most straightforward and I like it a lot for its elegance. It tries to reduce an arbitary $N$ to elementary values of $N$ that have been proven once. It works very nicely for even $N$, where we can reduce to $N=2$. The drawback is that we have to do all other $N$ separately.

Let us start with $N=4$ for simplicity. For $N=4$ the sum looks like this:

$$S = \sin^2\left(x\right) + \sin^2\left(x + \frac{\pi}{4}\right) + \sin^2\left(x + \frac{\pi}{2}\right) + \sin^2\left(x + \frac{3\pi}{4}\right)$$

Actually, the first and the third term look familiar. They represent the case $N=2$ which we assume proven. Let us rearrange the sum by exchanging second and third term:

$$S = \underbrace{\sin^2\left(x\right)  + \sin^2\left(x + \frac{\pi}{2}\right)}_{f_1(x)} + \underbrace{\sin^2\left(x + \frac{\pi}{4}\right) + \sin^2\left(x + \frac{3\pi}{4}\right)}_{f_2(x)}$$

Now, for $f_1(x)$ we know that $f_1(x) = 1, \; \forall x$ from the TPI. The key is to realize that $f_2(x)$ is actually a shifted copy of $f_1(x)$, i.e., $f_2(x) = f_1(x + \pi/4)$, since both arguments just get an “extra” $\pi/4$ to it (remember that $3/4\pi$ is nothing but $\pi/2 + \pi/4$).

Now it’s easy, we have:

$$ S = f_1(x) + f_2(x) = f_1(x) + f_1(x-\pi/4) = 1 + 1 = 2,$$

since $f_1(x) = 1, \; \forall x$.

 

Does this work for any even $N$? Sure! We always have $f_1(x)$ in there (the first and the $N/2$-th term) and all other terms are $\pi/N$ shifted versions of it. Mathematically:

\begin{align} & \sum_{n=0}^{N-1} \sin^2\left( x+ \frac{\pi}{N} n \right) \\
= & \sum_{n=0}^{N/2-1} \sin^2\left( x+ \frac{\pi}{N} n \right) + \sin^2\left( x+ \pi + \frac{\pi}{N} n \right) \\
= & \sum_{n=0}^{N/2-1} \sin^2\left( x+ \frac{\pi}{N} n \right) + \cos^2\left( x+ \frac{\pi}{N} n \right) \\
= & \sum_{n=0}^{N/2-1} f_1\left(x + \frac{\pi}{N} n\right) \\
= & \sum_{n=0}^{N/2-1} 1 = \frac{N}{2}. \end{align}

Piece of cake.

This is nice but here is the trouble: for odd $N$ it’s not so easy. It already breaks down for $N=3$ since $f_1(x)$ does not even appear there. Even if you prove it for $N=3$, you can use this to prove it for all integer multiples of $3$ but it will not work for $N=5$. In other words, you would have to do this for every prime number separately. Not very elegant.

In essence, in case you were thinking of induction here, this will not work. Increasing $N$ by one changes all terms in the sum so you cannot go from $N$ to $N+1$ (only from $N$ to $2N$).

So, to prove it for arbitrary $N$ we need something else. What is there?

Proof idea 2: Power series

Wikipedia suggests that the original TPI can be proven using the definition of sine and cosine via its power series, i.e.,

\begin{align}
\sin(x) & = \sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)!} x^{2n+1} \\
\cos(x) & = \sum_{n=0}^\infty \frac{(-1)^n}{(2n)!} x^{2n}
\end{align}

Based on these, you can find the power series for $\sin^2$ and $\cos^2$, then  sum them and find out that $n=0$ gives $0 + 1 = 1$ and all $n>0$ give $(1-1)^{2n} = 0$.

Oookay, to be honest I haven’t tried this approach for the extended TPI. I can imagine it would work but for sure it would be a lot of work and quite surely far away from being an elegant proof. In highschool, we referred to these as the “crowbar-type” solutions.

It’s one of the typical points where your favorite textbook might simply say: the details of the proof are left as an excercise to the reader. Go ahead and give it a shot if you like… 😉

 Proof idea 3: Differentiating

As usual, writing things down makes the whole thing much more clear and more often than not gives new ideas. I just thought about differentiating the whole sum. If we can show that the differential is zero everywhere we at least know that the sum is constant. We still have to calculate this constant for a complete answer of course.

To calculate the differential let us look at $\sin^2(x)$ for a second. Its differential satisfies a cute relation:

$$\frac{{\rm d} \sin^2(x)}{{\rm d} x} = 2 \sin(x) \cos(x) = \sin(2x).$$

Why cute? Well, look at it for a second. If I differentiate $x^2$ I get $2x$, the 2 goes from the exponent in front of it. If I differentiate $\sin^2(x)$ I get $\sin(2x)$, the 2 goes inside the sine function. But please be careful here, this is not a general rule! It is a pure coincidence, like a little joke made by nature. In fact, it neither works for $n>2$ nor does it work for the cosine, which satisfies

$$\frac{{\rm d} \cos^2(x)}{{\rm d} x} = -2 \sin(x) \cos(x) = -\sin(2x).$$

Now let us turn to our sum $S$. We get

$$ \frac{{\rm d} S}{{\rm d} x} = \sum_{n=0}^{N-1} \sin\left( 2x+ \frac{2\pi}{N} n \right),$$

which we claim should be zero everywhere. This is an interesting one: if you overlap a sine with all its shifted copies (shifts being uniformly chosen from $[0,2\pi)$), the net result is zero. This is something I’ve seen many times before, especially in its relation to complex numbers.

Here is one geometrical interpretation. From Euler’s identity, we have

$${\rm e}^{\jmath x} = \cos(x) + \jmath \sin(x).$$

Therefore, if we write the following sum

$$ \sum_{n=0}^{N-1} {\rm e}^{\jmath (x+\frac{2\pi}{N}n)}
= \sum_{n=0}^{N-1} \cos\left(x+\frac{2\pi}{N}n\right) + \jmath \sum_{n=0}^{N-1} \sin\left(x+\frac{2\pi}{N}n\right),$$

i.e., our desired sum appears in the imaginary part (besides for a factor 2 on the $x$ but this does not matter since our argument applies for any $x$ so it can be rescaled). I am claiming the whole (complex) sum is zero, which shows that our desired sum is zero. Why is that so? Let’s factor out ${\rm e}^{\jmath x}$:

$$ \sum_{n=0}^{N-1} {\rm e}^{\jmath (x+\frac{2\pi}{N}n}) =  {\rm e}^{\jmath x} \underbrace{\sum_{n=0}^{N-1} {\rm e}^{\jmath \frac{2\pi}{N}n}}_z.$$

Now, what is $z$? Imagine a complex plane. Every term in the sum for $z$ is a point on the unit circle, spaced evenly. You can imagine the sum like this: take arrows to all points on the unit circles and add them all together. Find the sum of all these arrows. What is the net direction that remains when we’ve gone in all directions there are evenly? Well, it cannot be any point other than zero. Here is a visualization for it:

The whole thing is completely symmetric so there cannot be any preferred direction. We must have $z=0$, which proves the whole thing.

Of course this is, while being illustrative, a little hand-wavy. There are many more ways to prove $z=0$ more rigorously. I’m not sure which is the most concise and elegant. Right now, I keep thinking about DFTs here, since ${\rm e}^{\jmath \frac{2\pi}{N}n}$ is actually the second row of the $N \times N$ DFT matrix, which makes $z=0$ equivalent to showing that the first and the second row of a DFT matrix are mutually orthogonal. At the same time, ${\rm e}^{\jmath \frac{2\pi}{N}n}$ is the DFT of the sequence $\delta[n-1] = [0,1,0,…,0]$ in which case $z=0$ follows from the fact that the sum of the DFT coefficients is always equal to the first value of the sequence. But that’s just what comes to my mind first, I guess there are easier ways to prove this.

So there you have it, if we differentiate the sum, it’s easy to show that it must be constant. However, this is not the complete proof of the extended TPI yet, we still have to compute the constant. I’m not sure that is easy to do for an arbitrary $N$, is it?

To conclude, so far

So, what do we have? A quite elegant proof for even $N$ that does not generalize to odd $N$, a possible tedious proof idea based on power series, and a sort-of elegant proof that the sum is constant for arbitrary $N$ which still lacks the computation of this constant.

Now I’m curious: do you have better ideas to prove it? Have you come across this or similar identities? Do you know if it has a name and where it has been proven first?

 

*Update*: I have found a generalization to sine functions raised to any even power $2k$ and also an elegant proof, which also proves the TPI discussed in this post. Check it out if you like.